Return Stacked® Portfolio Solutions
The “Rebalance Drag” Myth in Leveraged ETFs: What Advisors Need to Know
Overview
Key Topics
Return Stacking, Portfolio Enhancement, Portable Alpha, Institutional Implementation, Capital Efficiency, Behavioral Finance, Alternative Investment Integration, ETF Strategy
When discussing exchange-traded funds (ETFs), especially those using leverage, you’ll often hear about “rebalance drag.” This idea suggests that resetting or rebalancing a leveraged ETF’s exposure creates a performance drag over time. While leveraged products, particularly single-asset ETFs, often show lower returns than their unleveraged counterparts, this isn’t due to some mysterious “rebalancing penalty.” The real culprit is a well-known effect called variance drain, combined with the difference between simple average returns and actual compounded returns. Let’s break down why “rebalance drag” isn’t a real effect and what really matters for leveraged ETF performance.
Debunking the Myth of "Rebalance Drag"
The myth of “rebalance drag” often comes from misunderstanding how daily or periodic rebalancing works in leveraged ETFs. For instance, a 2x leveraged ETF aims to deliver twice the daily return of its underlying index. To maintain this target, the fund manager adjusts the exposure daily. If the underlying target goes up, the levered fund has to buy more; if underlying goes down, the levered fund has to sell. Some believe this process of “buying high and selling low” creates a long-term performance drag as markets bounce around.
However, any “drag” here isn’t about the rebalancing itself. It’s a direct result of the relationship between volatility and compounding returns. The confusion arises when people focus on rebalancing transactions as the cause of underperformance, rather than on variance drain—the difference between average returns and compounded returns—which increases with leverage in a single-asset context.
Rebalancing vs. Having a View on Relative Returns
When we talk about rebalancing in a multi-asset portfolio, we often hear terms like “rebalancing premium” or “rebalancing bonus.” This idea suggests that periodically rebalancing among uncorrelated assets can improve the portfolio’s growth rate. This isn’t magic; it’s about maintaining diversification and reducing overall portfolio volatility.
A rebalancing premium only happens if investors believe there’s some mean-reversion or difference in asset performance and if the assets have less than perfect correlation. You need (1) multiple assets with different expected returns or correlations, and (2) a reason to believe that rebalancing into “losers” and out of “winners” makes sense long-term. Rebalancing a single asset or between assets without favorable correlation won’t magically generate a premium. Without a strong view on relative returns or a diversification benefit, rebalancing alone doesn’t create excess returns.
The Real Culprit: Variance Drain
The real phenomenon often mistaken for “rebalance drag” is variance drain, also known as “volatility drag.” Variance drain is the mathematical fact that an investment’s compounded return is always less than or equal to its simple average return. The gap between these returns widens with higher volatility.
Arithmetic Return: The simple average of returns over multiple periods.
Geometric Return: The return that accounts for compounding, reflecting what investors actually experience.
For a volatile asset, the more its returns fluctuate, the larger the gap between the average return and the actual compounded return. If you leverage that asset, you magnify gains and losses, amplifying volatility. Higher volatility means bigger variance drain, and the compounded growth rate lags further behind the simple average.
This shortfall has nothing to do with daily rebalancing or leverage resets. Even with monthly or quarterly rebalancing, a leveraged single-asset portfolio would still suffer from variance drain. Compounding doesn’t care about rebalancing frequency; it cares about the volatility of the underlying returns.
Leverage and Its Impact on Returns
Leverage magnifies returns, both positively and negatively. A 2x leveraged fund linked to a single ETF will deliver roughly twice the daily moves of the index. In sustained growth periods with moderate volatility, this can significantly boost returns. However, in choppy or downward markets, the same leverage intensifies losses. Over time, these ups and downs compound to produce lower geometric returns than what a simple doubling of average returns might imply.
The key point is that leveraged single-asset ETFs inherently suffer not from “rebalance drag,” but from the variance drain that leverage amplifies. In other words, the drag arises from the interplay of volatility and compounding, not from rebalancing.
Shannon's Demon and Diversification
The “rebalancing premium” – which we would argue is better thought of as a “diversification premium” – is best seen in diversified portfolios with multiple uncorrelated or negatively correlated assets. Rebalancing here ensures each asset’s weight is periodically restored, effectively “selling high and buying low” across different return streams. When correlations are low, and each asset has a reasonable expected return, this strategy can lead to a higher compound growth rate than a simple weighted average of the assets’ returns.
Shannon’s Demon shows that with two or more uncorrelated assets with positive drift, continuously rebalancing between them can produce a higher compound return than holding them individually. This premium is sometimes wrongly attributed to rebalancing itself. It’s the combination of diversification and maintaining allocations across multiple assets with different returns that yields the advantage.
Concentrated vs. Diversified Leveraged ETFs
The impact of variance drag in concentrated leveraged ETFs and diversified leveraged ETFs can be meaningfully different.
Concentrated Leveraged ETFs apply leverage to a single asset or index, like a 2x S&P 500 ETF. With no diversification, the volatility of that single index is amplified, increasing variance drain. The long-run geometric return tends to underperform what naive math might predict. This underperformance isn’t due to rebalancing; it’s the result of compounding volatility.
Diversified Leveraged ETFs, on the other hand, use leverage across a basket of diversified assets, like a balanced stock-bond portfolio leveraged to 1.5x. If these assets have low correlation and positive expected returns, the portfolio may experience less variance drain than a single concentrated asset. Effective diversification can keep overall volatility moderate, potentially achieving higher geometric growth. Rebalancing here helps maintain target allocations, producing a more favorable risk-return profile than a single concentrated levered asset.
Register for our Advisor Center
Tools Center:
Easily backtest & explore different return stacking concepts
Model Portfolios:
Return stacked allocations, commentary and guidance designed
for a range of client risk profiles and goals
Future Thinking:
Receive up-to-date insights into the world of return stacking theory and practice
Simulation Insights: Visualizing Rebalancing, Variance Drain, and the Power of Diversified Leverage
To better understand how rebalancing and variance drain impact investment returns, we’ve created an interactive simulation tool. This tool allows you to generate multiple scenarios and visualize the performance of different assets over time. Additionally, we’ve analyzed the long-term performance implications of rebalancing using a broader set of simulations, the results of which are summarized in the density and bar plots. Let’s break down what the simulation and plots show, paying special attention to the role of leverage and how it interacts with diversification and rebalancing.
Understanding the Simulation
The interactive simulation generates paths for four different investment scenarios, all starting with $100:
- Asset 1 (solid dark line): Represents a single asset with a defined level of volatility (15% annualized in this case) and a specific average return.
- Asset 2 (dotted blue line): Similar to Asset 1, but its price movements are completely independent. It also has the same level of vol and the same average return.
- Asset A Levered 2x (light green line): This takes Asset 1 and applies 2x leverage to its daily returns. This means that if Asset 1 goes up 1%, this fund goes up 2%. If it goes down 1%, this fund goes down 2%.
- Two Uncorrelated (teal line): Represents the result of combining Asset 1 and Asset 2 and applying the same overall leverage as in the “Asset A Levered 2x” scenario. The leverage is achieved by holding equal weights of Asset 1 and Asset 2, and taking a 2x notional position in each. The portfolio is rebalanced daily, so that they have equal weight each day. This portfolio has a net leverage of 2x, constructed as 1 + 1.
Key Parameters
- Volatility: We’ve set the annualized volatility to 15% for both Asset 1 and Asset 2. Volatility measures how much an asset’s price fluctuates over time. The higher the volatility, the more “swingy” the asset’s performance.
- Annual Mean Return: Both assets have an annual mean return of 4.5%. This is the average return we expect each asset to generate over a year. Since we’ve assumed a 15% volatility, this is equivalent to a Sharpe Ratio of 0.3. Because the simulation assumes that the returns on the assets are normally distributed, the Sharpe ratio is a measure of how much return the asset generates per unit of volatility.
- Correlation: Asset 1 and Asset 2 are designed to be uncorrelated, meaning their price movements are independent of each other. This is important for illustrating the benefits of diversification.
- Rebalancing: The “Two Uncorrelated” portfolio is rebalanced daily. This means that at the end of each day, the portfolio is adjusted to maintain an equal weighting between Asset 1 and Asset 2.
What to Look For in the Interactive Simulation
When you click the “Generate New Comparison” button, the simulation creates a new set of random paths for each of the four scenarios. Pay close attention to these patterns:
-
-
Variance Drain in Leveraged Asset: Notice how the “Asset A Levered 2x” line (light green) tends to be more volatile than the “Asset 1” line (solid dark line). In periods where the underlying asset (Asset 1) declines, the leveraged version often performs much worse. And although it also goes up faster when the underlying asset rises, over the long term it tends to underperform what you might expect from simply doubling the returns of Asset 1. This is variance drain in action. The effect is particularly noticeable because of the leverage employed.
-
Benefits of Diversification with Leverage: This is where things get interesting. Compare the “Two Uncorrelated” line (teal) to the “Asset A Levered 2x” line (light green). Both portfolios have the same overall leverage (2x), but the “Two Uncorrelated” portfolio achieves this through diversification (holding two uncorrelated assets) rather than concentrating leverage on a single asset. You’ll often see that the “Two Uncorrelated” portfolio, while still volatile due to leverage, has a smoother ride and potentially better long-term performance than the concentrated “Asset A Levered 2x” portfolio. This highlights the power of using diversification to mitigate the negative impacts of variance drain when employing leverage.
-
Rebalancing in Action: The “Two Uncorrelated” portfolio demonstrates the effect of daily rebalancing. When one asset outperforms, the rebalancing mechanism sells a portion of it and buys more of the underperforming asset. This “sell high, buy low” strategy, combined with diversification, can lead to improved compounded returns over time, especially when assets are uncorrelated and leverage is involved.
-
Analyzing Long-Term Performance: Density and Bar Plots
To understand the long-term performance implications of rebalancing and diversified leverage, we ran the simulation 10,000 times, each time simulating a 10-year investment period with the same parameters as the interactive simulation (15% annualized volatility, 4.5% annual mean return, zero correlation, and daily rebalancing). We then compared the Compound Annual Growth Rate (CAGR) of the rebalanced portfolio (“Two Uncorrelated”) to a non-rebalanced portfolio with the same assets and leverage.
The results of these 10,000 simulations are summarized in the density plot and the bar plot:
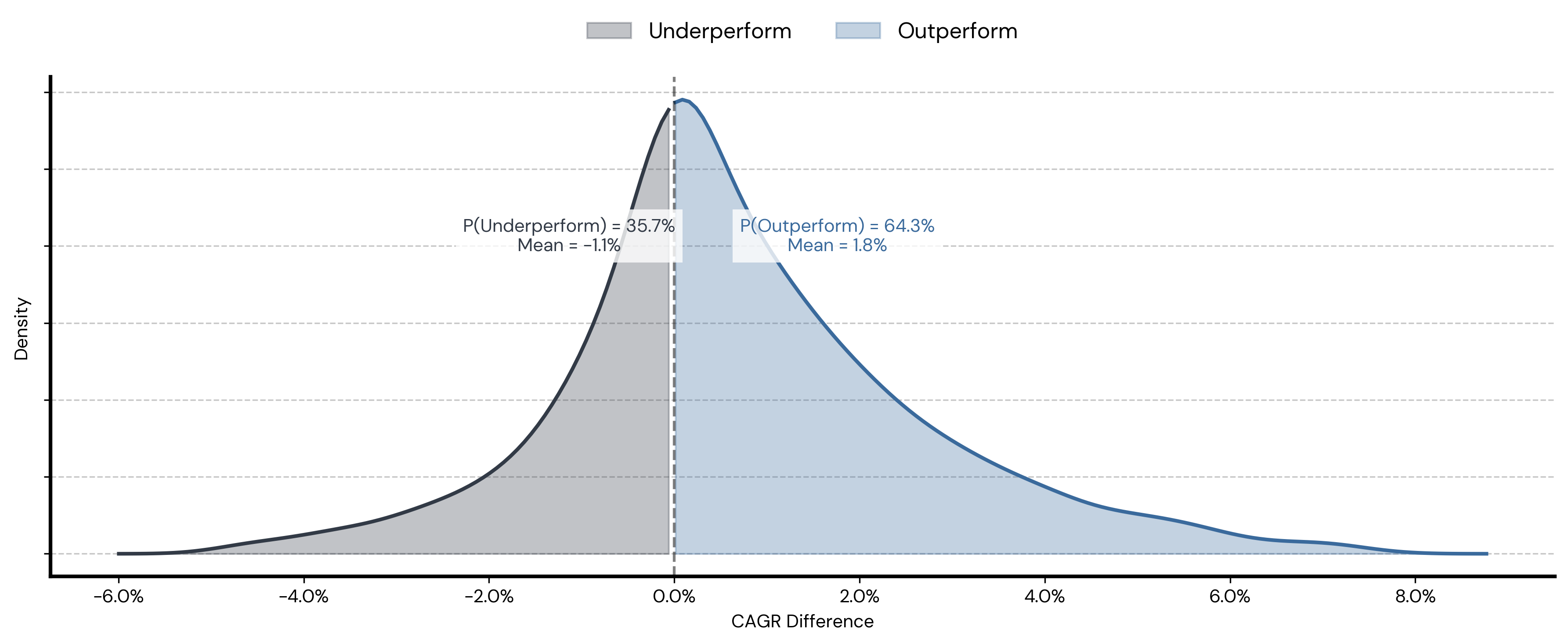
- Density Plot: This plot shows the distribution of the difference in CAGR between the rebalanced and non-rebalanced portfolios (both with 2x leverage, achieved either through concentration or diversification). A positive difference means the rebalanced portfolio outperformed. The plot reveals that the rebalanced portfolio outperformed in 64.3% of the simulations (P(Outperform) = 64.3%). This suggests that, under these conditions, rebalancing tends to add value over the long term, even when leverage is involved.
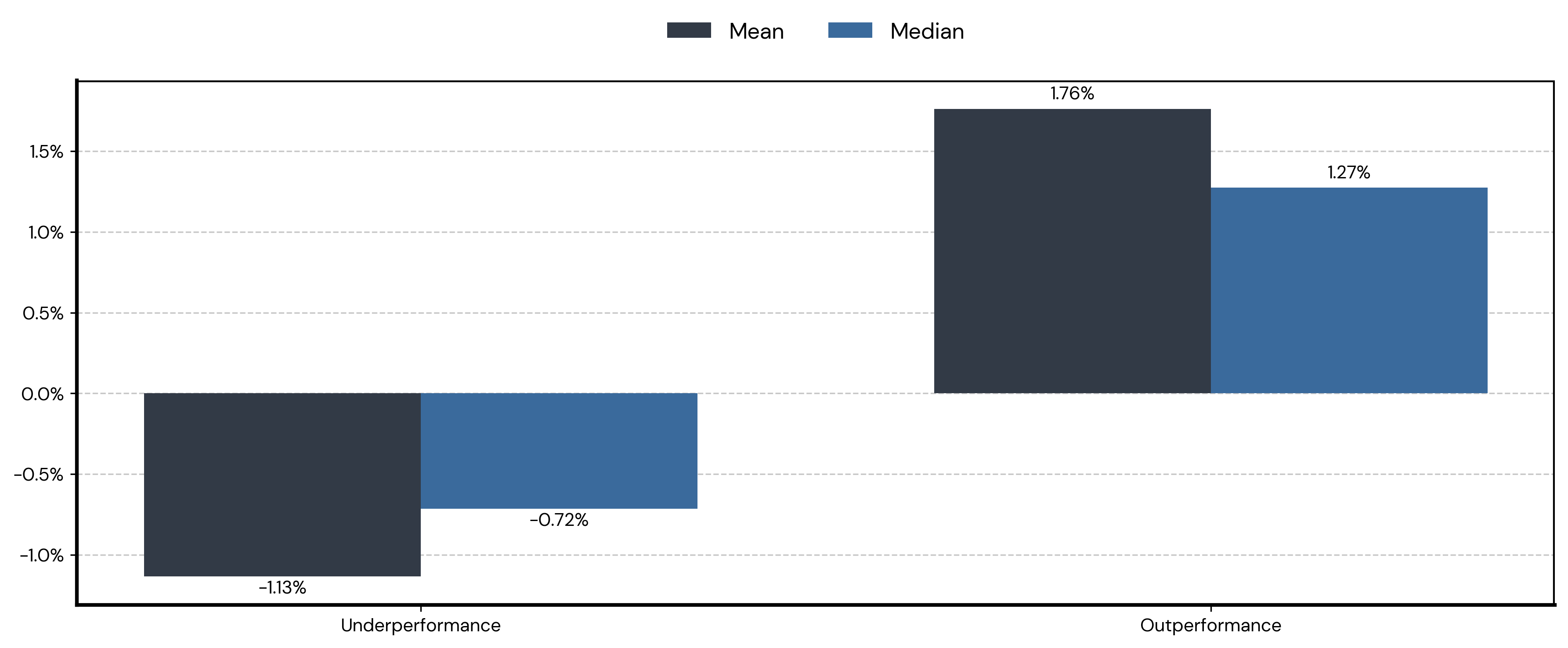
- Bar Plot: This plot shows the average magnitude of underperformance and outperformance. When the rebalanced portfolio underperformed, it did so by an average of -1.13% in terms of CAGR. However, when it outperformed, it did so by a larger average margin of 1.76%. The median underperformance and outperformance were -0.72% and 1.27% respectively. This indicates that the gains from rebalancing, when they occur, tend to be larger than the losses.
Interpreting the Results
The interactive simulation, combined with the long-term performance analysis from the density and bar plots, help visualize the key takeaways:
- Variance drain is a real effect, especially with leveraged assets. The higher volatility of leveraged assets leads to a larger gap between simple average returns and actual compounded returns. This is clearly visible in the interactive simulation, particularly when comparing “Asset A Levered 2x” to “Asset 1.”
- Rebalancing doesn’t cause a “drag” in itself. The act of rebalancing is simply a mechanism to maintain a target allocation.
- Diversification and rebalancing can improve long-term returns, especially when leverage is employed. The density plot, based on 10,000 simulations, demonstrates that a rebalanced portfolio with diversified leverage tends to add value over the long run, with a 64.3% probability of outperformance. The bar plot further reinforces this by showing that the average outperformance (1.76%) is larger in magnitude than the average underperformance (-1.13%). The interactive simulation visually demonstrates how a diversified leveraged portfolio (“Two Uncorrelated”) can potentially outperform a concentrated leveraged portfolio (“Asset A Levered 2x”) due to the mitigating effects of diversification on variance drain.
Experiment and Learn
Click the “Generate New Comparison” button in the interactive simulation multiple times to see how different random scenarios play out. Observe how the relationships between the lines change, paying particular attention to the two leveraged portfolios. Combine this with the insights from the density and bar plots, which represent a broader statistical analysis. This will give you a more intuitive understanding of variance drain, diversification, the impact of rebalancing, and, importantly, how these factors interact when leverage is used. The simulation and plots provide a simplified model, but they effectively illustrate the core concepts that every investor should understand when dealing with leveraged ETFs and multi-asset portfolios.
Advanced Simulation: Exploring the Impact of Key Parameters on Rebalancing
While the initial simulation provides a good starting point for understanding the dynamics of rebalancing and variance drain, it’s based on fixed parameters. To gain a deeper understanding of how different market conditions and portfolio choices affect the “rebalancing premium,” we’ve developed a more advanced simulator. This tool allows you to adjust key parameters and see their impact on long-term performance.
Return Stacked® Rebalancing Premium Simulator
Explore the impact of portfolio rebalancing under different market conditions
Simulation Parameters
Asset Parameters
Key Parameters You Can Adjust
- Number of Simulations: Run anywhere from 100 to 10,000 simulations to see how the distribution of outcomes changes with sample size.
- Investment Horizon: Explore investment periods ranging from 1 to 30 years.
- Rebalance Frequency: Choose from daily, weekly, monthly, quarterly, or annual rebalancing to see how frequency impacts results.
- Sharpe Ratio: Adjust the Sharpe ratio for both the “Core” and “Stack” assets. The Sharpe ratio is a measure of risk-adjusted return, calculated as (Return – Risk-Free Rate) / Volatility. A higher Sharpe ratio generally indicates a more attractive investment.
- Volatility: Set the volatility for both assets, representing the degree of price fluctuation.
- Correlation: Define the correlation between the two assets, ranging from -1 (perfectly negatively correlated) to +1 (perfectly positively correlated). A correlation of 0 means the assets move independently.
- Asset Weights: Specify the target weights for the “Core” and “Stack” assets in the portfolio. These weights determine the overall leverage and diversification of the portfolio.
What to Look For
As you experiment with different parameter combinations, pay close attention to the following metrics and visualizations:
-
- Mean CAGR Difference: This shows the average difference in Compound Annual Growth Rate between the rebalanced and non-rebalanced portfolios. A positive value indicates that rebalancing, on average, added value.
- Probability of Outperformance: This metric tells you the percentage of simulations where the rebalanced portfolio outperformed the non-rebalanced one.
- Average Underperformance/Outperformance: These values show the average magnitude of underperformance and outperformance when they occurred.
- Density Plot: This plot visualizes the distribution of CAGR differences between the rebalanced and non-rebalanced portfolios. It helps you understand the range of possible outcomes and the likelihood of different levels of outperformance or underperformance.
Insights to Explore
Here are some key relationships to investigate using the advanced simulator:
- Impact of Correlation: How does the correlation between the “Core” and “Stack” assets affect the rebalancing premium? What happens when assets are highly correlated, uncorrelated, or negatively correlated?
- Role of Volatility: How does changing the volatility of the assets impact the effectiveness of rebalancing? What’s the relationship between volatility, variance drain, and the rebalancing premium?
- Sharpe Ratio and Rebalancing: How does the Sharpe ratio of the assets influence the benefits of rebalancing? Does rebalancing add more value when assets have higher or lower Sharpe ratios?
- Leverage and Diversification: How do the weights of the “Core” and “Stack” assets affect the portfolio’s overall leverage and diversification? How does changing these weights impact the rebalancing premium and the probability of outperformance?
- Rebalance Frequency: Does the frequency of rebalancing (daily, weekly, monthly, etc.) significantly change the outcomes? Is there an optimal rebalancing frequency for different market conditions?
By systematically adjusting the parameters and observing the results, you’ll gain a much deeper understanding of the complex interplay between rebalancing, diversification, leverage, and market conditions. This knowledge will help you make more informed decisions when constructing and managing portfolios, especially those involving leveraged or multi-asset strategies.
Conclusion
The debate over “rebalance drag” in leveraged ETFs often confuses the act of resetting leverage with the mathematical phenomenon of variance drain. Daily or periodic rebalancing to restore a leverage ratio doesn’t inherently create a drag. The real reason leveraged single-asset ETFs may underperform is variance drain—the gap between average and compounded returns, which grows as volatility increases.
The “rebalancing premium” in multi-asset strategies isn’t about rebalancing transactions but about maintaining diversification and using the interplay between multiple, less-than-perfectly-correlated return streams. Without a strong view on relative returns and a correlation benefit, rebalancing alone won’t help. When leveraging a well-diversified portfolio, rebalancing can enhance the compound growth rate by mitigating volatility through consistent allocation maintenance.
Ultimately, it’s crucial to differentiate the real driver of performance in levered ETFs (variance drain from volatility) from the mechanical process of rebalancing. Whether you’re investing in a single-asset 2x or 3x ETF or a levered diversified portfolio, it’s not the resetting of leverage that harms returns, but the arithmetic of compounding that penalizes high volatility. Understanding this distinction helps investors make more informed decisions about using leveraged products and dispels the myth that “rebalance drag” is a separate force eroding returns.
